数据: 10 个目标点, 1 个基站,最大续航 20 分钟,风场为方向惩罚。
目标:最小化 \frac{总飞行时间}{风险惩罚} ;越界罚 \times10。
编码:[序列 |分隔符】(分隔符切分多段表示补给返回),或“指派向量 + 局部 2-opt "。
算子:OX交叉 + 2-opt /交换变异;精英保留 1-2 个。
可视化:
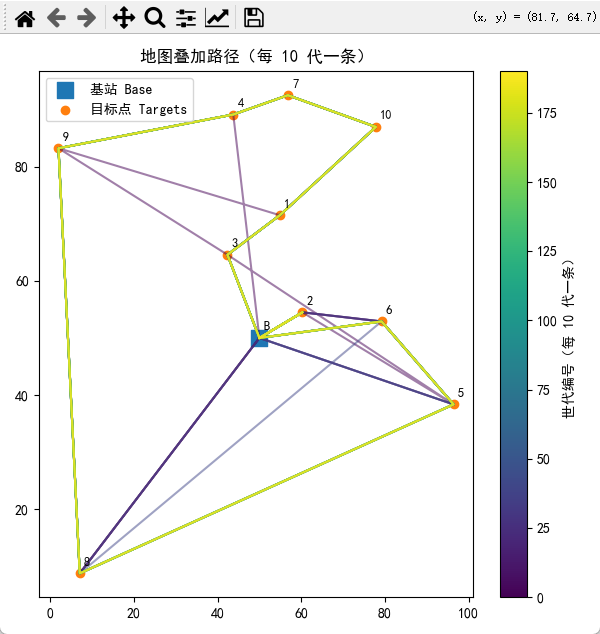
。地图叠加路径(每 10 代更新一次);
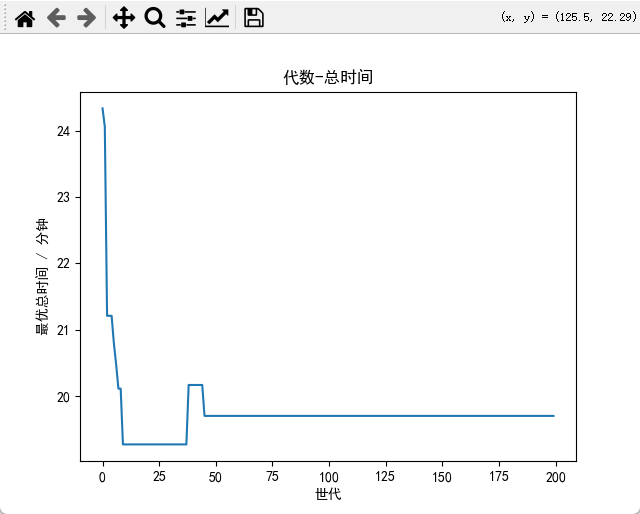
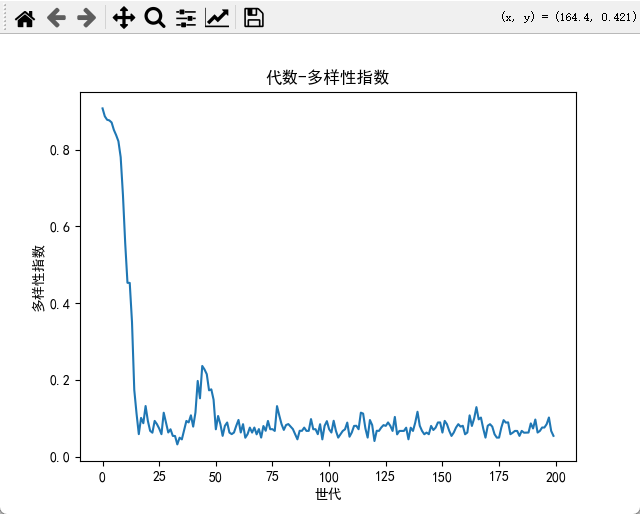
。曲线;代数-总时间;代数-多样性指数。
思考题:风向改变后,需要如何调参( p_m 、 精英数 、 2-opt 强度 )?
代码
import numpy as np
import matplotlib.pyplot as plt
# ========= 中文正常显示 =========
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# ===================== 1. 问题设置:10 个目标 + 1 个基站 =====================
np.random.seed(0)
num_targets = 10
num_points = num_targets + 1 # + 基站
MAX_TRIPS = 2 # 最多 2 段出航(1 个分隔符)
SEP = 0 # 分隔符基因,用 0 表示
# 基站设在中心 (50, 50),目标点随机撒在 [0, 100] × [0, 100]
base = np.array([[50.0, 50.0]])
targets = np.random.rand(num_targets, 2) * 100
points = np.vstack([base, targets]) # points[0] 是基站,1..10 是目标点
# ---------- 风场参数:统一风向 + 方向惩罚 ----------
# 设一个大致向右上角吹的风
wind_dir = np.array([1.0, 0.5], dtype=float)
wind_dir = wind_dir / np.linalg.norm(wind_dir)
alpha = 0.3 # 风对时间的影响强度:0 表示无风
# ---------- 风险场:离中心越远越危险 ----------
center = np.array([50.0, 50.0], dtype=float)
max_radius = np.linalg.norm(np.array([0.0, 0.0], dtype=float) - center)
gamma = 0.5 # 风险程度系数:0.5 → 最危险区域的风险因子约为 0.5
# ---------- 续航约束 ----------
time_per_unit = 0.04 # 每 1 个距离单位耗时 0.04 分钟
endurance_minutes = 20.0 # 最大续航时间
boundary_penalty_factor = 10.0 # 越界罚 10x(作用在时间上)
# ========== 染色体解码 & 评价 ==========
def decode_trips(ind, sep=SEP):
"""
将染色体 decode 为若干段出航序列。
例如 ind = [3,8,5,7,0,2,1,9,10,4,6]
返回 [[3,8,5,7], [2,1,9,10,4,6]]
"""
trips = []
cur = []
for g in ind:
if g == sep:
if cur:
trips.append(cur)
cur = []
else:
cur.append(int(g))
if cur:
trips.append(cur)
return trips
def compute_segment_metrics(perm):
"""
计算单段出航(Base -> perm -> Base)的指标:
- raw_time:真实飞行时间(考虑风,但不含罚)
- eff_time:用于优化的“有效时间”(若 >20 分钟则乘 10)
- risk_factor:风险因子 (0,1],越小越危险
"""
path_idx = np.concatenate([[0], perm, [0]])
coords = points[path_idx]
total_dist = 0.0
raw_time = 0.0
risk_factors = []
for i in range(len(coords) - 1):
p = coords[i]
q = coords[i + 1]
seg_vec = q - p
dist = float(np.linalg.norm(seg_vec))
if dist == 0.0:
continue
total_dist += dist
# ----- 风场方向惩罚 -----
d_unit = seg_vec / dist
cos_theta = float(np.dot(d_unit, wind_dir))
cos_theta = max(-1.0, min(1.0, cos_theta))
# cos_theta = 1 顺风;cos_theta = -1 逆风
wind_factor = 1.0 + alpha * (1.0 - cos_theta)
seg_time = dist * time_per_unit * wind_factor
raw_time += seg_time
# ----- 风险:离中心越远越危险 -----
mid = 0.5 * (p + q)
r = float(np.linalg.norm(mid - center) / max_radius)
r = max(0.0, min(1.0, r))
seg_risk = 1.0 - gamma * r # ∈ [1-gamma,1]
risk_factors.append(seg_risk)
if risk_factors:
risk_factor = sum(risk_factors) / len(risk_factors)
else:
risk_factor = 1.0
# 超过续航时间 → 时间乘以 10
if raw_time > endurance_minutes:
eff_time = raw_time * boundary_penalty_factor
else:
eff_time = raw_time
return total_dist, raw_time, eff_time, risk_factor
def compute_route_metrics_multi(ind):
"""
计算多段出航的总指标:
返回:
- total_dist: 总距离
- total_raw_time: 不含罚的总时间(分钟)
- global_risk: 平均风险因子
- objective: 目标值 = 总有效时间 / global_risk
"""
trips = decode_trips(ind)
if not trips:
return 0.0, 0.0, 1.0, 1e9
total_dist = 0.0
total_raw_time = 0.0
total_eff_time = 0.0
risk_sum = 0.0
seg_cnt = 0
for seg in trips:
perm = np.array(seg, dtype=int)
dist, raw_t, eff_t, risk = compute_segment_metrics(perm)
total_dist += dist
total_raw_time += raw_t
total_eff_time += eff_t
risk_sum += risk
seg_cnt += 1
global_risk = risk_sum / seg_cnt if seg_cnt > 0 else 1.0
objective = total_eff_time / global_risk
return total_dist, total_raw_time, global_risk, objective
# ===================== 2. GA 算法([序列|分隔符] + OX 交叉 + 交换变异) =====================
pop_size = 80
n_generations = 200
pc = 0.9 # 交叉概率
pm = 0.2 # 变异概率
def init_population():
"""
染色体基因为 1..num_targets 再加 (MAX_TRIPS-1) 个分隔符 0,
然后做一次全排列。
MAX_TRIPS=2 时只有一个分隔符,对 OX 交叉友好(基因不重复)。
"""
genes = np.concatenate([
np.arange(1, num_points, dtype=int),
np.array([SEP] * (MAX_TRIPS - 1), dtype=int)
])
pop = []
for _ in range(pop_size):
perm = np.random.permutation(genes)
pop.append(perm)
return np.array(pop, dtype=int)
def fitness(ind):
"""
适应度:目标值越小越好,所以取其倒数。
"""
_, _, _, obj = compute_route_metrics_multi(ind)
return 1.0 / (obj + 1e-6)
def tournament_selection(pop, k=3):
idx = np.random.randint(0, len(pop), size=k)
cand = pop[idx]
fit = np.array([fitness(ind) for ind in cand])
return cand[fit.argmax()].copy()
def ordered_crossover(p1, p2):
"""
OX 交叉:在 [序列|分隔符] 编码上也可用(前提是基因不重复)。
"""
n = len(p1)
c1, c2 = np.sort(np.random.choice(n, 2, replace=False))
child = -np.ones(n, dtype=int)
# 中段来自 p1
child[c1:c2 + 1] = p1[c1:c2 + 1]
# 剩余位置按顺序从 p2 填充
rest = [x for x in p2 if x not in child]
j = 0
for i in range(n):
if child[i] == -1:
child[i] = rest[j]
j += 1
return child
def swap_mutation(ind):
"""
简单交换变异:随机交换两个位置的基因(包括可能交换分隔符)。
"""
a, b = np.random.choice(len(ind), 2, replace=False)
ind[a], ind[b] = ind[b], ind[a]
def population_diversity(pop):
"""
多样性指数:所有个体两两平均汉明距离 / 染色体长度 ∈ [0,1]
"""
pop_arr = np.array(pop)
n, L = pop_arr.shape
if n < 2:
return 0.0
dist_sum = 0
cnt = 0
for i in range(n):
for j in range(i + 1, n):
dist_sum += np.sum(pop_arr[i] != pop_arr[j])
cnt += 1
return dist_sum / (cnt * L)
# ===================== 3. 主循环:记录用于可视化的数据 =====================
pop = init_population()
best_times = [] # 每代最优的“总飞行时间(未罚)”
best_objs = [] # 每代最优目标值(含罚)
diversities = [] # 每代多样性
snapshots = {} # 每 10 代保存一条最优解,画地图用
# 👉 一定要在这里初始化全局最优
global_best_obj = float("inf")
global_best_time = None
global_best_dist = None
global_best_risk = None
global_best_ind = None
global_best_gen = None
for gen in range(n_generations):
metrics = [compute_route_metrics_multi(ind) for ind in pop]
times = np.array([m[1] for m in metrics]) # total_raw_time
objs = np.array([m[3] for m in metrics]) # objective
best_idx = objs.argmin()
best_times.append(times[best_idx])
best_objs.append(objs[best_idx])
diversities.append(population_diversity(pop))
# ---- 更新全局最优解(跨所有世代)----
if objs[best_idx] < global_best_obj:
global_best_obj = objs[best_idx]
global_best_time = times[best_idx]
global_best_dist = metrics[best_idx][0] # total_dist
global_best_risk = metrics[best_idx][2] # global_risk
global_best_ind = pop[best_idx].copy()
global_best_gen = gen
if gen % 10 == 0:
snapshots[gen] = pop[best_idx].copy()
# ---- 精英保留 1 个 ----
elite = pop[best_idx].copy()
# ---- 选择 + 交叉 + 变异 ----
new_pop = [elite] # 把精英先塞进去
while len(new_pop) < pop_size:
p1 = tournament_selection(pop)
p2 = tournament_selection(pop)
if np.random.rand() < pc:
c1 = ordered_crossover(p1, p2)
c2 = ordered_crossover(p2, p1)
else:
c1, c2 = p1.copy(), p2.copy()
if np.random.rand() < pm:
swap_mutation(c1)
if np.random.rand() < pm:
swap_mutation(c2)
new_pop.append(c1)
if len(new_pop) < pop_size:
new_pop.append(c2)
pop = np.array(new_pop, dtype=int)
# ===================== 打印更具体的计算信息 =====================
print("======== 全局最优解统计结果 ========")
print(f"出现世代: {global_best_gen}")
print(f"最优染色体编码: {global_best_ind}")
print(f"出航分段(decode_trips): {decode_trips(global_best_ind)}")
print(f"总飞行距离: {global_best_dist:.3f}")
print(f"总飞行时间(未罚): {global_best_time:.3f} 分钟")
print(f"平均风险因子: {global_best_risk:.3f}")
print(f"最终最优目标值: {global_best_obj:.3f}")
print("\n---- 各段出航详细信息 ----")
trips = decode_trips(global_best_ind)
sum_seg_dist = 0.0
sum_seg_time = 0.0
for i, seg in enumerate(trips, start=1):
seg_list = [int(x) for x in seg] # 纯 Python int,用来打印
seg_arr = np.array(seg_list, dtype=int) # Numpy 数组,用来计算
seg_dist, seg_raw_t, seg_eff_t, seg_risk = compute_segment_metrics(seg_arr)
penalized = "是" if seg_eff_t > seg_raw_t + 1e-9 else "否"
sum_seg_dist += seg_dist
sum_seg_time += seg_raw_t
print(f"第 {i} 段: 访问顺序 {seg_list}")
print(f" 本段总距离 = {seg_dist:.3f}")
print(f" 本段原始时间 = {seg_raw_t:.3f} 分钟")
print(f" 本段有效时间(含超续航罚) = {seg_eff_t:.3f} 分钟, 是否触发10x罚: {penalized}")
print(f" 本段平均风险因子 = {seg_risk:.3f}")
# ================== 这里是你要的“子段细节” ==================
path_idx = np.concatenate([[0], seg_arr, [0]]) # Base -> ... -> Base 的索引序列
coords = points[path_idx]
print(" 子段明细:")
for j in range(len(coords) - 1):
p_idx = path_idx[j]
q_idx = path_idx[j + 1]
p = coords[j]
q = coords[j + 1]
vec = q - p
dist = float(np.linalg.norm(vec))
if dist == 0.0:
sub_time = 0.0
sub_risk = 0.0
else:
# 和 compute_segment_metrics 完全一致的时间 / 风险计算
d_unit = vec / dist
cos_theta = float(np.dot(d_unit, wind_dir))
cos_theta = max(-1.0, min(1.0, cos_theta))
wind_factor = 1.0 + alpha * (1.0 - cos_theta)
sub_time = dist * time_per_unit * wind_factor
mid = 0.5 * (p + q)
r = float(np.linalg.norm(mid - center) / max_radius)
r = max(0.0, min(1.0, r))
sub_risk = 1.0 - gamma * r
from_label = "Base" if p_idx == 0 else str(p_idx)
to_label = "Base" if q_idx == 0 else str(q_idx)
print(f" {from_label} -> {to_label}: 距离 = {dist:.3f}, 时间 = {sub_time:.3f} 分钟, 风险因子 = {sub_risk:.3f}")
# ==========================================================
print(f" 当前累计距离 = {sum_seg_dist:.3f},当前累计时间 = {sum_seg_time:.3f} 分钟\n")
print("---- 按段累加的汇总值(用于和全局结果对比) ----")
print(f"分段距离之和 = {sum_seg_dist:.3f},全局总飞行距离 = {global_best_dist:.3f}")
print(f"分段时间之和 = {sum_seg_time:.3f},全局总飞行时间 = {global_best_time:.3f} 分钟")
# ===================== 4. 可视化 =====================
# 4.1 地图叠加路径(每 10 代一条)
gens = sorted(snapshots.keys())
colors = plt.cm.viridis(np.linspace(0, 1, len(gens)))
fig, ax = plt.subplots(figsize=(6, 6))
# 基站和目标点
base_scatter = ax.scatter(points[0, 0], points[0, 1], marker='s', s=120)
targets_scatter = ax.scatter(points[1:, 0], points[1:, 1])
# ==== 在这里给每个点加编号 ====
for i, (x, y) in enumerate(points):
if i == 0:
label = "B" # 或者写成 "0"、"Base" 都行
else:
label = str(i) # 目标点 1..10
ax.text(x + 1, y + 1, # 略微偏移一点,避免挡住点
label,
fontsize=9,
color="black",
ha="left", va="bottom",
zorder=5)
# =================================
# 每 10 代一条路径(可能包含多段出航)
for gen, color in zip(gens, colors):
ind = snapshots[gen]
trips = decode_trips(ind)
for seg in trips:
path_idx = np.concatenate([[0], seg, [0]])
ax.plot(points[path_idx, 0],
points[path_idx, 1],
color=color,
alpha=0.5)
ax.set_title("地图叠加路径(每 10 代一条)")
# 图例只显示“基站 / 目标”
ax.legend([base_scatter, targets_scatter],
["基站 Base", "目标点 Targets"],
loc="upper left")
# 用 colorbar 表示是哪一代的路径
sm = plt.cm.ScalarMappable(cmap=plt.cm.viridis,
norm=plt.Normalize(vmin=min(gens), vmax=max(gens)))
sm.set_array([])
cbar = plt.colorbar(sm, ax=ax)
cbar.set_label("世代编号(每 10 代一条)")
plt.tight_layout()
# 4.2 代数-总飞行时间(未罚)
plt.figure()
plt.plot(best_times)
plt.xlabel("世代")
plt.ylabel("最优总时间 / 分钟")
plt.title("代数-总时间")
# 4.3 代数-多样性指数
plt.figure()
plt.plot(diversities)
plt.xlabel("世代")
plt.ylabel("多样性指数")
plt.title("代数-多样性指数")
plt.show()
======== 全局最优解统计结果 ========
出现世代: 45
最优染色体编码: [ 3 1 10 7 4 9 8 5 6 0 2]
出航分段(decode_trips): [[3, 1, 10, 7, 4, 9, 8, 5, 6], [2]]
总飞行距离: 378.846
总飞行时间(未罚): 19.700 分钟
平均风险因子: 0.869
最终最优目标值: 22.667
---- 各段出航详细信息 ----
第 1 段: 访问顺序 [3, 1, 10, 7, 4, 9, 8, 5, 6]
本段总距离 = 356.419
本段原始时间 = 18.534 分钟
本段有效时间(含超续航罚) = 18.534 分钟, 是否触发10x罚: 否
本段平均风险因子 = 0.778
子段明细:
Base -> 3: 距离 = 16.466, 时间 = 0.860 分钟, 风险因子 = 0.942
3 -> 1: 距离 = 14.306, 时间 = 0.572 分钟, 风险因子 = 0.872
1 -> 10: 距离 = 27.671, 时间 = 1.110 分钟, 风险因子 = 0.763
10 -> 7: 距离 = 21.734, 时间 = 1.326 分钟, 风险因子 = 0.693
7 -> 4: 距离 = 13.477, 时间 = 0.859 分钟, 风险因子 = 0.711
4 -> 9: 距离 = 42.154, 时间 = 2.672 分钟, 风险因子 = 0.680
9 -> 8: 距离 = 74.722, 时间 = 4.231 分钟, 风险因子 = 0.677
8 -> 5: 距离 = 94.052, 时间 = 3.774 分钟, 风险因子 = 0.812
5 -> 6: 距离 = 22.521, 时间 = 1.278 分钟, 风险因子 = 0.731
6 -> Base: 距离 = 29.315, 时间 = 1.853 分钟, 风险因子 = 0.896
当前累计距离 = 356.419,当前累计时间 = 18.534 分钟
第 2 段: 访问顺序 [2]
本段总距离 = 22.427
本段原始时间 = 1.166 分钟
本段有效时间(含超续航罚) = 1.166 分钟, 是否触发10x罚: 否
本段平均风险因子 = 0.960
子段明细:
Base -> 2: 距离 = 11.214, 时间 = 0.449 分钟, 风险因子 = 0.960
2 -> Base: 距离 = 11.214, 时间 = 0.717 分钟, 风险因子 = 0.960
当前累计距离 = 378.846,当前累计时间 = 19.700 分钟
---- 按段累加的汇总值(用于和全局结果对比) ----
分段距离之和 = 378.846,全局总飞行距离 = 378.846
分段时间之和 = 19.700,全局总飞行时间 = 19.700 分钟可视化
思考题
-
提高变异率( P_m )
-
风向一变,原来“顺风段”可能变成“逆风段”,旧解质量大幅下降。
-
适当 提高变异概率、或在若干代里加大变异幅度,让种群跳出旧的路径模式,多尝试新的航线组合。
-
-
暂时减少精英数
-
之前的精英个体是在旧风向下得到的,很可能已经“过时”。
-
减少精英保留(比如由 2 个减到 0–1 个),避免旧精英长期占据大量选择概率,妨碍种群向新环境适应。
-
-
先减弱,后加强 2-opt 强度
-
2-opt 是局部搜索 / 局部优化算子,强度越大,当前解越容易被“磨”进一个局部最优。
-
风向刚变时:先把 2-opt 做得弱一些,让 GA 先多探索新路径;
-
若干代之后:种群已经在新风向下收敛到一个区域,再把 2-opt 强度调回去(甚至略微增强),精细打磨航线。
-

