数据: 3 台机器、 5 个作业,工序顺序给定。
目标:最小化 Makespan。
编码:操作级排列(每个作业的工序按出现次数判定)。
算子:PHX/0X + 插入/逆序变异,修复器保证设备占用不神突。
可视化:
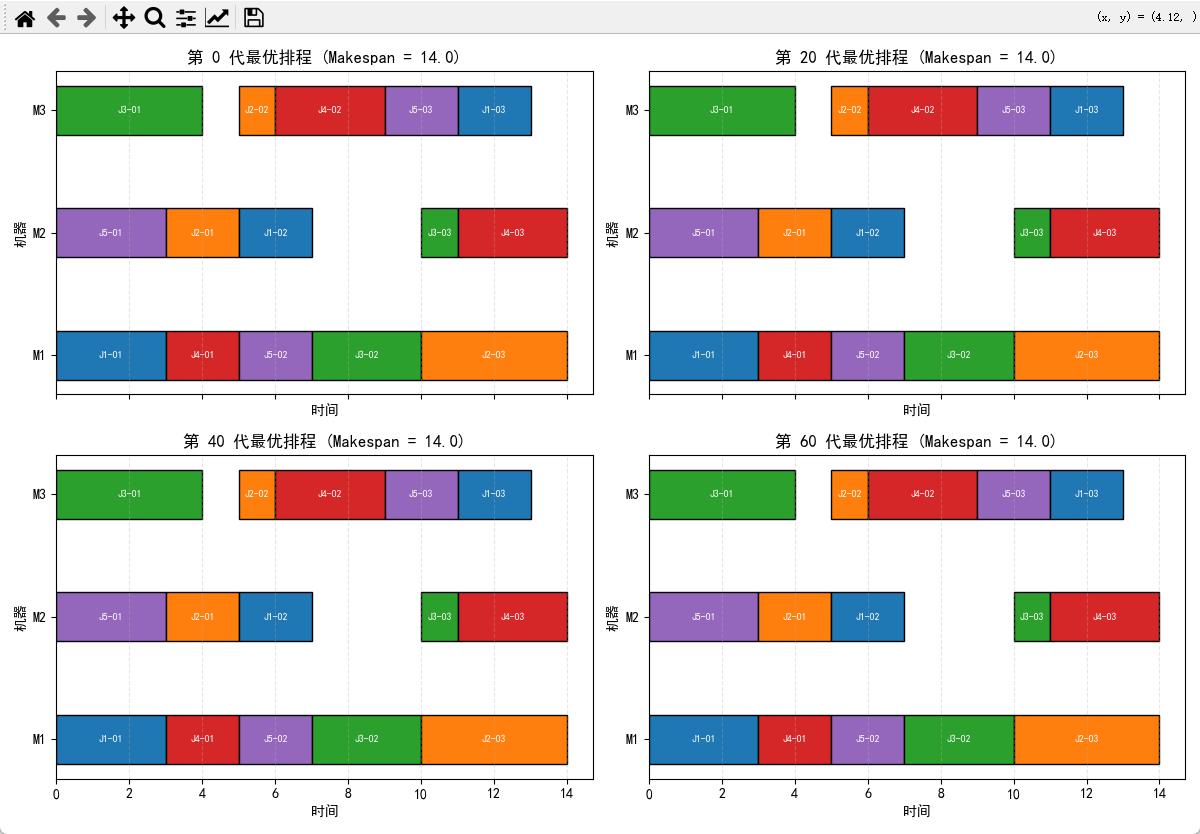
甘特图对比“第 0、20、40、60 代最优排程”
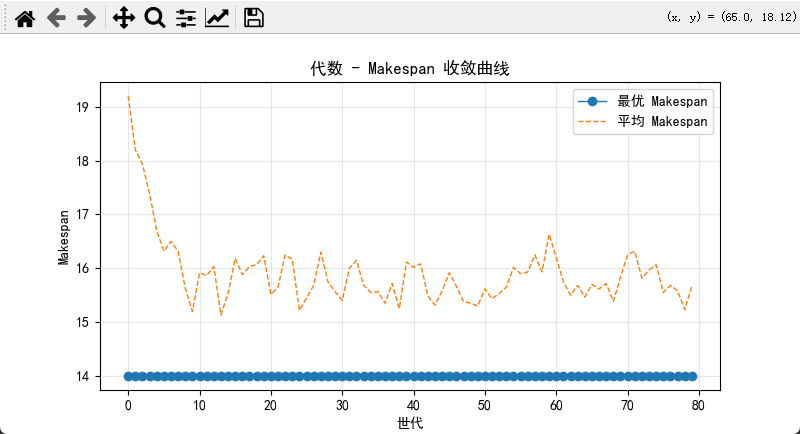
代数-Makespan 折线。
讨论:无修复器直接罚分 vs 有修复器强合法,谁更快收?为什么?
代码
import numpy as np
import matplotlib.pyplot as plt
import math
# ========= 中文正常显示 =========
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# ===================== 1. 数据:3 台机器,5 个作业 =====================
# 每个作业是一串 (machine, processing_time) 的工序序列
# ⚠️ 这里是【示例数据】;如果老师给了具体表,直接改 jobs_ops 即可。
num_machines = 3
jobs_ops = {
# 作业 0:在 M1 上加工 3 时间,然后 M2 上 2 时间,然后 M3 上 2 时间
0: [(0, 3), (1, 2), (2, 2)],
# 作业 1:M2 上 2,M3 上 1,M1 上 4
1: [(1, 2), (2, 1), (0, 4)],
# 作业 2:M3 上 4,M1 上 3,M2 上 1
2: [(2, 4), (0, 3), (1, 1)],
# 作业 3:M1 上 2,M3 上 3,M2 上 3
3: [(0, 2), (2, 3), (1, 3)],
# 作业 4:M2 上 3,M1 上 2,M3 上 2
4: [(1, 3), (0, 2), (2, 2)],
}
num_jobs = len(jobs_ops)
# 每个作业有多少道工序
ops_per_job = {j: len(jobs_ops[j]) for j in jobs_ops}
total_ops = sum(ops_per_job.values()) # 仅供参考,不强制使用
# ===================== 2. 解码:操作级排列 -> 具体排程 =====================
def decode_schedule(chrom):
"""
chrom: 长度 total_ops 的数组,每个位置是 job_id(0~4),
每出现一次就表示该作业的“下一道工序”。
解码规则:
- 对每个作业 j,工序顺序固定:jobs_ops[j][0], jobs_ops[j][1], ...
- 扫描 chrom,每遇到一次 j,就取该作业的下一道工序,
按“作业前序约束 + 机器占用约束”计算 start/end。
→ 天然保证排程合法,相当于带一个“修复器”。
"""
# 记录该作业下一个要执行第几道工序
job_next = {j: 0 for j in jobs_ops}
# 作业和机器的就绪时间
job_ready = {j: 0.0 for j in jobs_ops}
mach_ready = {m: 0.0 for m in range(num_machines)}
schedule = [] # 每个元素:{'job', 'op_index', 'machine', 'start', 'end'}
for job_id in chrom:
j = int(job_id)
op_idx = job_next[j] # 该作业的第几道工序
m, p = jobs_ops[j][op_idx] # 需要的机器 & 工时
start = max(job_ready[j], mach_ready[m])
end = start + p
job_ready[j] = end
mach_ready[m] = end
job_next[j] += 1
schedule.append({
'job': j,
'op_index': op_idx,
'machine': m,
'start': start,
'end': end,
})
makespan = max(job_ready.values())
return makespan, schedule
# ===================== 3. GA 算子:适应度 / 选择 / 交叉 / 变异 =====================
def fitness(chrom):
# 目标是最小化 Makespan → 适应度取其倒数
ms, _ = decode_schedule(chrom)
return 1.0 / (ms + 1e-6)
def init_population(pop_size):
"""
操作级排列:每个作业 j 出现 ops_per_job[j] 次,打乱顺序。
如:3 台机 5 作业,每个作业 3 道工序 → 序列长度 15。
"""
base_seq = []
for j in range(num_jobs):
base_seq.extend([j] * ops_per_job[j])
base_seq = np.array(base_seq, dtype=int)
pop = [np.random.permutation(base_seq) for _ in range(pop_size)]
return np.array(pop, dtype=int)
def tournament_selection(pop, k=3):
"""锦标赛选择。"""
idx = np.random.randint(0, len(pop), size=k)
cand = pop[idx]
fits = np.array([fitness(ind) for ind in cand])
return cand[fits.argmax()].copy()
def job_based_ox(p1, p2):
"""
“作业顺序交叉”(Job-based OX 变种),兼容多重基因:
- 随机选一个片段,从 p1 拷贝过来;
- 其余位置按 p2 的顺序填充,保证每个作业出现次数仍为 ops_per_job[j]。
"""
n = len(p1)
c1, c2 = sorted(np.random.choice(n, 2, replace=False))
child = np.full(n, -1, dtype=int)
# 每个作业还剩多少次可以放
need = ops_per_job.copy()
# 片段来自 p1
for idx in range(c1, c2 + 1):
g = int(p1[idx])
if need[g] > 0:
child[idx] = g
need[g] -= 1
# 剩余位置按 p2 顺序填满
for g in p2:
g = int(g)
if need[g] > 0:
pos = np.where(child == -1)[0][0]
child[pos] = g
need[g] -= 1
return child
def insertion_mutation(ind):
"""插入变异:随机拿出一个基因,插入到另一位置。"""
n = len(ind)
i, j = np.random.choice(n, 2, replace=False)
arr = ind.tolist()
gene = arr.pop(i)
arr.insert(j, gene)
ind[:] = np.array(arr, dtype=int)
def reverse_mutation(ind):
"""逆序变异:随机选一个区间,整段反转。"""
n = len(ind)
i, j = np.random.choice(n, 2, replace=False)
if i > j:
i, j = j, i
ind[i:j + 1] = ind[i:j + 1][::-1]
# ===================== 4. GA 主循环 + 记录可视化数据 =====================
def ga_jobshop(pop_size=60, n_generations=80, pc=0.9, pm=0.2):
pop = init_population(pop_size)
best_makespans = [] # 每代最优 Makespan
avg_makespans = [] # 每代平均 Makespan
global_best_ms = math.inf
global_best_ind = None
snapshot_gens = [0, 20, 40, 60]
snapshots = {} # gen -> best individual
for gen in range(n_generations):
# ---- 评价当前种群 ----
ms_list = []
for ind in pop:
ms, _ = decode_schedule(ind)
ms_list.append(ms)
ms_arr = np.array(ms_list)
best_idx = ms_arr.argmin()
best_ms = ms_arr[best_idx]
best_makespans.append(best_ms)
avg_makespans.append(ms_arr.mean())
# 更新全局最优
if best_ms < global_best_ms:
global_best_ms = best_ms
global_best_ind = pop[best_idx].copy()
# 记录 0/20/40/60 代最优个体,用于画甘特图
if gen in snapshot_gens and gen not in snapshots:
snapshots[gen] = pop[best_idx].copy()
# ---- 精英保留 + 选择 + 交叉 + 变异 ----
elite = pop[best_idx].copy()
new_pop = [elite]
while len(new_pop) < pop_size:
p1 = tournament_selection(pop)
p2 = tournament_selection(pop)
# 交叉
if np.random.rand() < pc:
c1 = job_based_ox(p1, p2)
c2 = job_based_ox(p2, p1)
else:
c1, c2 = p1.copy(), p2.copy()
# 变异:插入 或 逆序
if np.random.rand() < pm:
if np.random.rand() < 0.5:
insertion_mutation(c1)
else:
reverse_mutation(c1)
if np.random.rand() < pm:
if np.random.rand() < 0.5:
insertion_mutation(c2)
else:
reverse_mutation(c2)
new_pop.append(c1)
if len(new_pop) < pop_size:
new_pop.append(c2)
pop = np.array(new_pop, dtype=int)
return global_best_ms, global_best_ind, best_makespans, avg_makespans, snapshots
# ===================== 5. 可视化:甘特图 + 代数-Makespan 折线 =====================
def plot_gantt(schedule, title, ax):
"""
简单甘特图:
y 轴是机器 M1/M2/M3,bar 颜色区分作业,标签显示 Jx-Oy。
"""
cmap = plt.cm.tab10
job_colors = {j: cmap(j % 10) for j in range(num_jobs)}
for op in schedule:
j = op['job']
m = op['machine']
start = op['start']
end = op['end']
ax.barh(
y=m,
left=start,
width=end - start,
height=0.4,
color=job_colors[j],
edgecolor='black'
)
ax.text(
(start + end) / 2,
m,
f"J{j + 1}-O{op['op_index'] + 1}",
ha='center',
va='center',
fontsize=7,
color='white'
)
ax.set_yticks(range(num_machines))
ax.set_yticklabels([f"M{m + 1}" for m in range(num_machines)])
ax.set_xlabel("时间")
ax.set_ylabel("机器")
ax.set_title(title)
ax.grid(True, axis='x', linestyle='--', alpha=0.3)
if __name__ == "__main__":
np.random.seed(0)
best_ms, best_ind, best_makespans, avg_makespans, snapshots = ga_jobshop()
print("======== 全局最优排程结果 ========")
print("最优 Makespan:", best_ms)
print("最优染色体(作业序列):", best_ind)
# 画 0 / 20 / 40 / 60 代最优甘特图
fig, axes = plt.subplots(2, 2, figsize=(12, 8), sharex=True)
gens_to_plot = [0, 20, 40, 60]
for ax, gen in zip(axes.ravel(), gens_to_plot):
ind = snapshots[gen]
ms, schedule = decode_schedule(ind)
plot_gantt(schedule, f"第 {gen} 代最优排程 (Makespan = {ms})", ax)
plt.tight_layout()
# 画 “代数 - Makespan” 收敛曲线(最优 + 平均)
plt.figure(figsize=(8, 4))
plt.plot(best_makespans, marker='o', linewidth=1, label="最优 Makespan")
plt.plot(avg_makespans, linestyle='--', linewidth=1, label="平均 Makespan")
plt.xlabel("世代")
plt.ylabel("Makespan")
plt.title("代数 - Makespan 收敛曲线")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
======== 全局最优排程结果 ========
最优 Makespan: 14.0
最优染色体(作业序列): [0 3 2 4 1 1 4 3 0 2 4 2 1 3 0]可视化
思考题
在这个实现里,其实解码过程本身就相当于一个“修复器”:
-
无论染色体里作业顺序多乱,
decode_schedule都会按照「作业前后顺序 + 机器单占」来调度每一步,
生成的一定是合法、不冲突的排程。 -
也就是说,GA 只在“合法排程空间”里搜索,不会产生“机器重叠、作业跳步骤”的解。
如果你不用这种 decode/修复,而是直接给每个操作随便一个开始时间、然后:
-
机器冲突就加一个大罚分;
-
或者作业次序违规也罚分;
那会发生两件事:
-
大量个体是严重非法解,适应度全是大罚分,几乎分不出好坏。
→ 选择算子看见的都是“差不多一样糟糕”的解,进化方向就很模糊。 -
搜索空间极大,而且绝大部分区域是“非法+被罚”的沼泽。
→ GA 花了很多代在沼泽里乱跳,真正高质量的合法解很稀少,收敛就慢。
而“强制修复”(本题这种解码方式)直接把所有染色体映射到最近的合法排程,结果是:
-
适应度差别主要反映了“工序顺序好不好”,而不是“有没有冲突”。
-
搜索空间从“合法 + 大量非法”收缩成“全是合法的时间表”,
目标函数更平滑,选择压力更清晰,GA 更容易朝好解方向爬。
所以一般来说:
有修复器的 GA(强制合法)会比单纯罚分的 GA 收敛更快、更稳定。
罚分法常见的问题是——罚分系数不好调,太小不收敛,太大全被淹没。
现在这份代码,其实就是“带修复器版本”的一个干净实现:
染色体只负责“作业访问顺序”,所有“资源冲突 + 工序约束”都在解码阶段一次性处理掉。

