Q-learning+ε-greedy
Q-learing原理
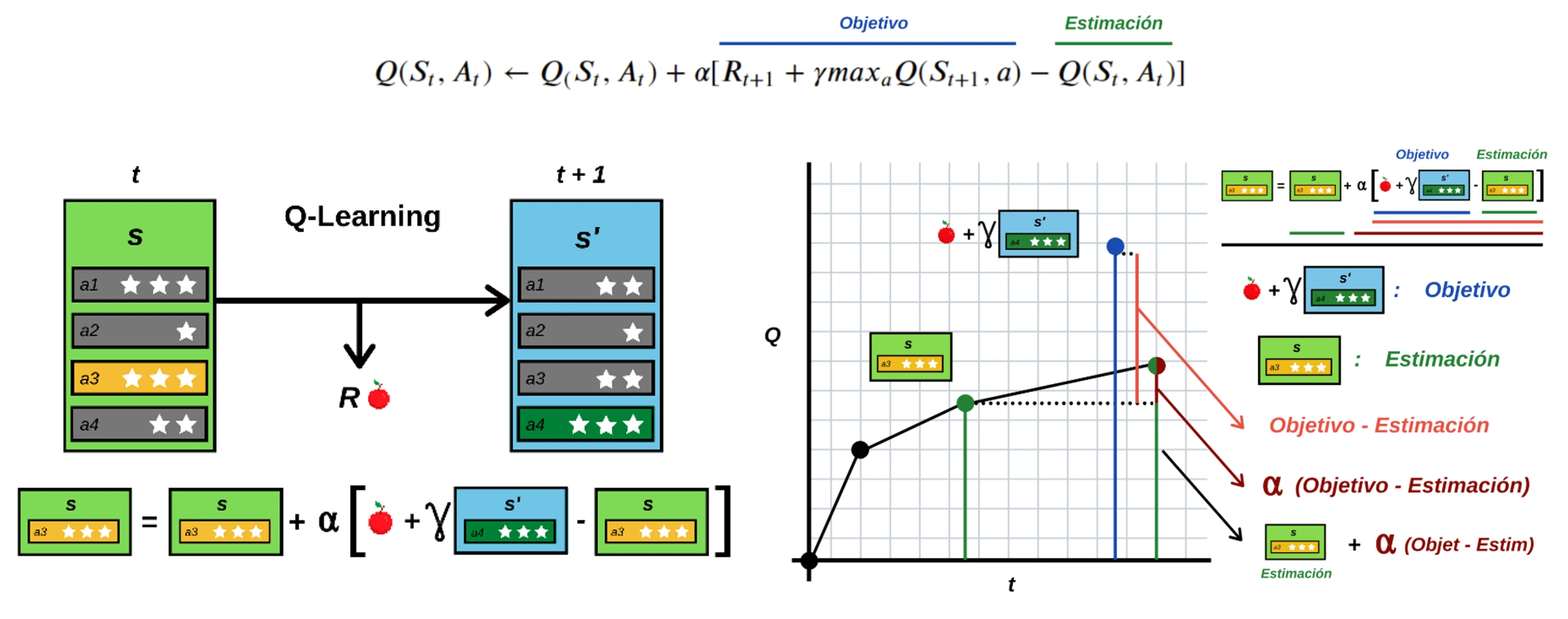
为什么要用 ε-greedy
在强化学习中,智能体(Agent)面临两个选择:
-
利用 (Exploitation):根据当前学到的知识(Q表),选择分数最高的动作,以获取已知最大的奖励。
-
探索 (Exploration):尝试未知的或分数较低的动作,希望能发现更好的策略(虽然可能会暂时亏损)。
如果只利用(纯贪婪),智能体可能陷入局部最优,永远找不到最佳路径;如果只探索,智能体永远无法利用学到的知识。
\epsilon-greedy 提供了一个简单的平衡方案:
-
以1-\epsilon 的概率:选择当前 Q 值最高的动作(利用)。
-
以\epsilon 的概率:随机选择一个动作(探索)。
任务
-
使用 gymnasium
-
实现 Q-learning +ε-greedy 搜索
-
展示训练曲线与智能体路径改善
输出要求
-
学习曲线:Episode vs RetuIn
-
路径示意图(至少 3 次不同时间点)
-
100 字讨论:探索率。ε对结果的影响
代码
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
# 实现epsilon-greedy策略选择动作
# 参数:Q值表、当前状态s、探索率eps、动作空间大小nA、随机数生成器rng
# 原理:以概率eps随机选择动作,否则选择Q值最大的动作
def epsilon_greedy(Q, s, eps, nA, rng):
if rng.random() < eps:
return rng.integers(nA)
return int(np.argmax(Q[s]))
# 使用当前Q表执行一条贪心轨迹,并返回轨迹和总奖励
def rollout_greedy(env, Q, max_steps=200, seed=0):
rng = np.random.default_rng(seed)
s, _ = env.reset(seed=int(rng.integers(1_000_000)))
path = [s]
total_r = 0.0
for _ in range(max_steps):
a = int(np.argmax(Q[s]))
s2, r, terminated, truncated, _ = env.step(a)
total_r += r
path.append(s2)
s = s2
if terminated or truncated:
break
return path, total_r
def draw_trajectory_cliffwalking(env, path, title, save_path):
H, W = env.unwrapped.shape # (4, 12)
# state -> (row, col)
def rc(state):
return divmod(int(state), W)
# 背景:cliff 区域
grid = np.zeros((H, W), dtype=float)
grid[H-1, 1:W-1] = -1 # cliff
# 把轨迹点标在 grid 上
for st in path:
r, c = rc(st)
grid[r, c] = 0.5
sr, sc = rc(path[0])
gr, gc = rc(path[-1])
plt.figure()
plt.imshow(grid, interpolation="nearest")
# 画路径连线(用格子中心点)
xs, ys = [], []
for st in path:
r, c = rc(st)
xs.append(c)
ys.append(r)
plt.plot(xs, ys)
plt.scatter([sc], [sr], marker="o")
plt.scatter([gc], [gr], marker="x")
plt.title(title)
plt.gca().invert_yaxis()
plt.xticks(range(W))
plt.yticks(range(H))
plt.grid(True, linewidth=0.5)
plt.tight_layout()
plt.savefig(save_path, dpi=200)
plt.close()
# 实现Q-learning算法训练
# alpha:学习率 gamma:折扣因子 eps_start/eps_end:初始和最终探索率 eps_decay:探索率衰减系数
def train_q_learning(
env_name="CliffWalking-v1",
episodes=5000,
alpha=0.1,
gamma=0.99,
eps_start=1.0,
eps_end=0.05,
eps_decay=0.999,
seed=42,
checkpoints=(50, 500, 3000),
):
env = gym.make(env_name)
nS = env.observation_space.n
nA = env.action_space.n
Q = np.zeros((nS, nA), dtype=np.float32)
rng = np.random.default_rng(seed)
returns = []
saved_Q = {} # episode -> Q snapshot
eps = eps_start
for ep in range(1, episodes + 1):
s, _ = env.reset(seed=int(rng.integers(1_000_000)))
done = False
G = 0.0
while not done:
a = epsilon_greedy(Q, s, eps, nA, rng)
s2, r, terminated, truncated, _ = env.step(a)
done = terminated or truncated
# Q-learning update
td_target = r + (0.0 if done else gamma * np.max(Q[s2]))
Q[s, a] += alpha * (td_target - Q[s, a])
s = s2
G += r
returns.append(G)
# epsilon decay
eps = max(eps_end, eps * eps_decay)
if ep in checkpoints:
saved_Q[ep] = Q.copy()
env.close()
return Q, np.array(returns, dtype=np.float32), saved_Q
def plot_learning_curve(returns, save_path="learning_curve.png", window=50):
plt.figure()
plt.plot(np.arange(1, len(returns) + 1), returns, linewidth=1)
if len(returns) >= window:
ma = np.convolve(returns, np.ones(window)/window, mode="valid")
plt.plot(np.arange(window, len(returns) + 1), ma, linewidth=2)
plt.xlabel("Episode")
plt.ylabel("Return")
plt.title("Episode vs Return (Q-learning + epsilon-greedy)")
plt.tight_layout()
plt.savefig(save_path, dpi=200)
plt.close()
if __name__ == "__main__":
env_name = "CliffWalking-v1"
episodes = 5000
checkpoints = (50, 500, 3000) # 至少 3 次不同时间点
Q, returns, saved_Q = train_q_learning(
env_name=env_name,
episodes=episodes,
alpha=0.1,
gamma=0.99,
eps_start=1.0,
eps_end=0.05,
eps_decay=0.999,
seed=42,
checkpoints=checkpoints,
)
# 1) 学习曲线
plot_learning_curve(returns, save_path="learning_curve.png", window=50)
print("Saved: learning_curve.png")
# 2) 轨迹示意图(3个时间点)
env = gym.make(env_name)
for ep in checkpoints:
path, G = rollout_greedy(env, saved_Q[ep], seed=ep)
out = f"traj_ep{ep}.png"
draw_trajectory_cliffwalking(env, path, f"Greedy Trajectory @ Episode {ep} (Return={G:.1f})", out)
print("Saved:", out)
# 3) 最终策略轨迹(可选)
path, G = rollout_greedy(env, Q, seed=2025)
draw_trajectory_cliffwalking(env, path, f"Final Greedy Trajectory (Return={G:.1f})", "traj_final.png")
print("Saved: traj_final.png")
env.close()
可视化
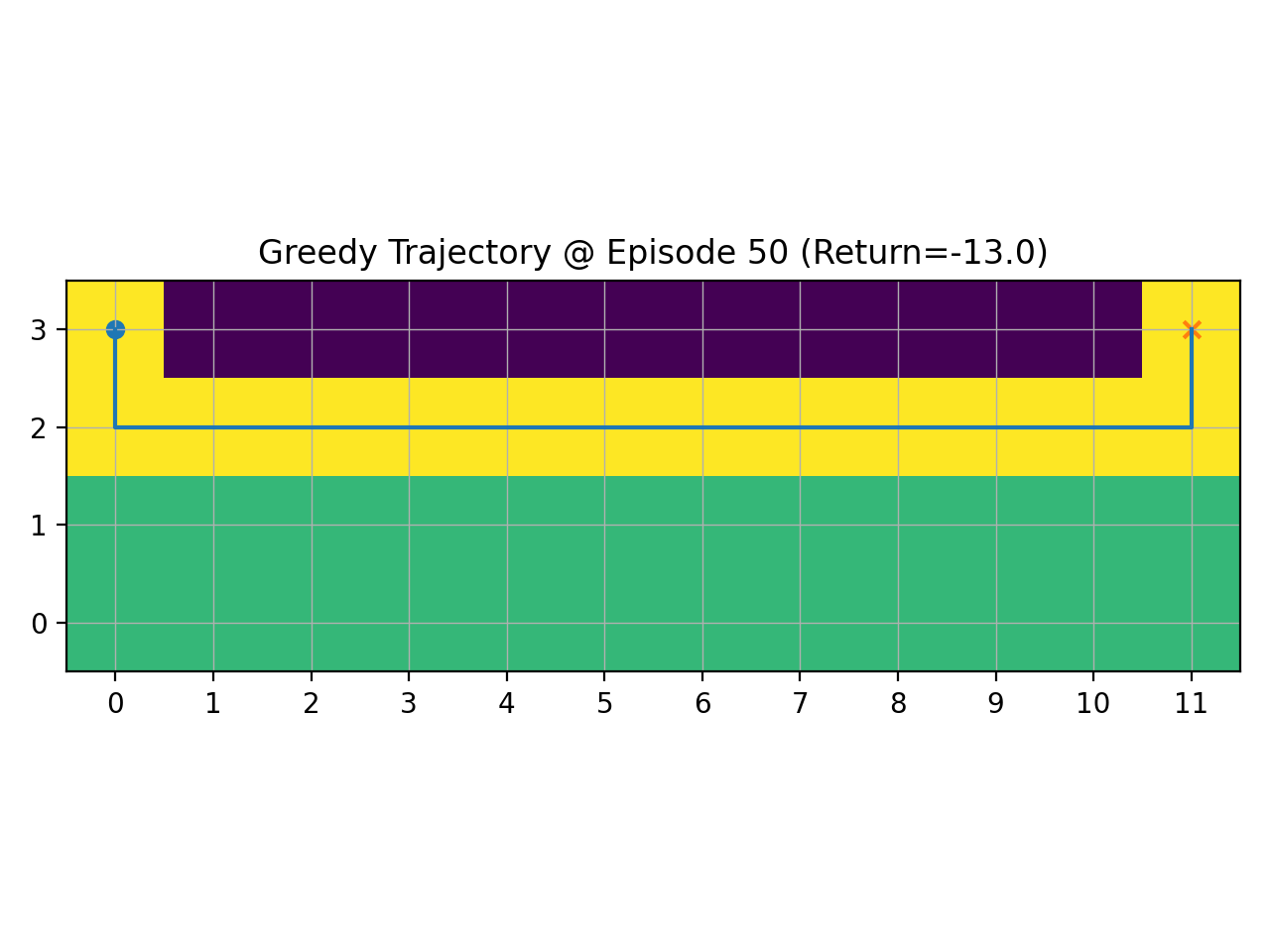
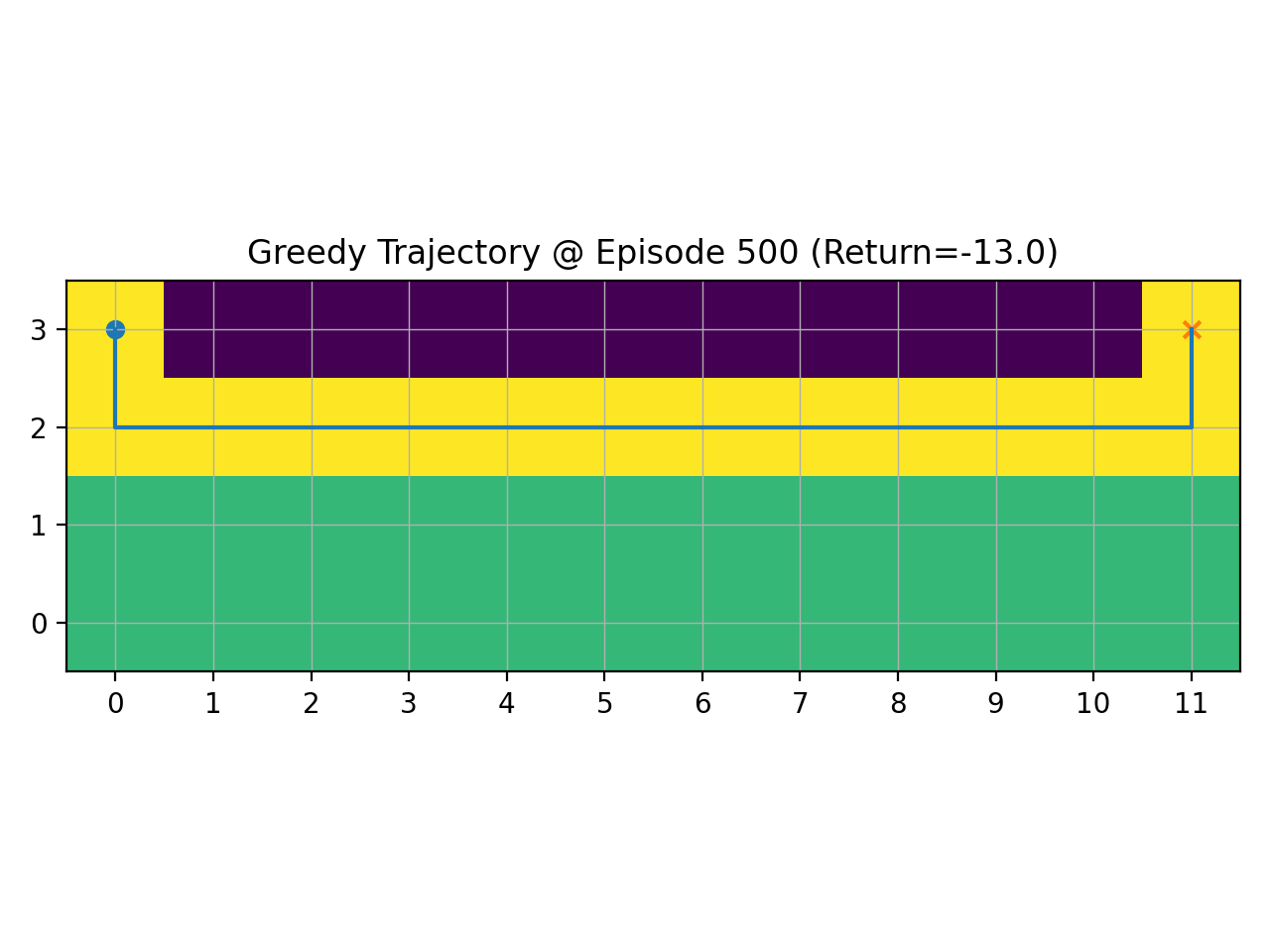
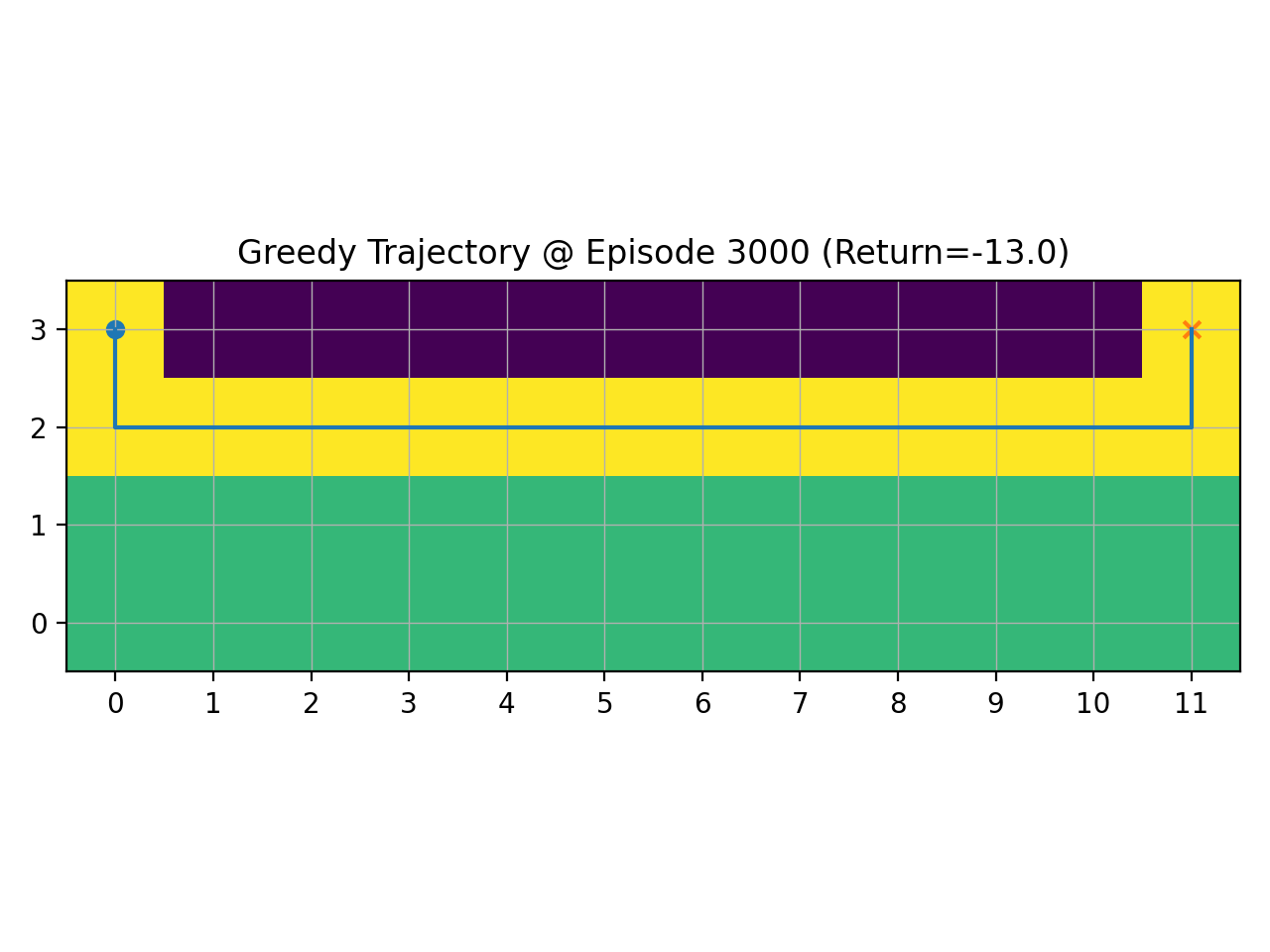
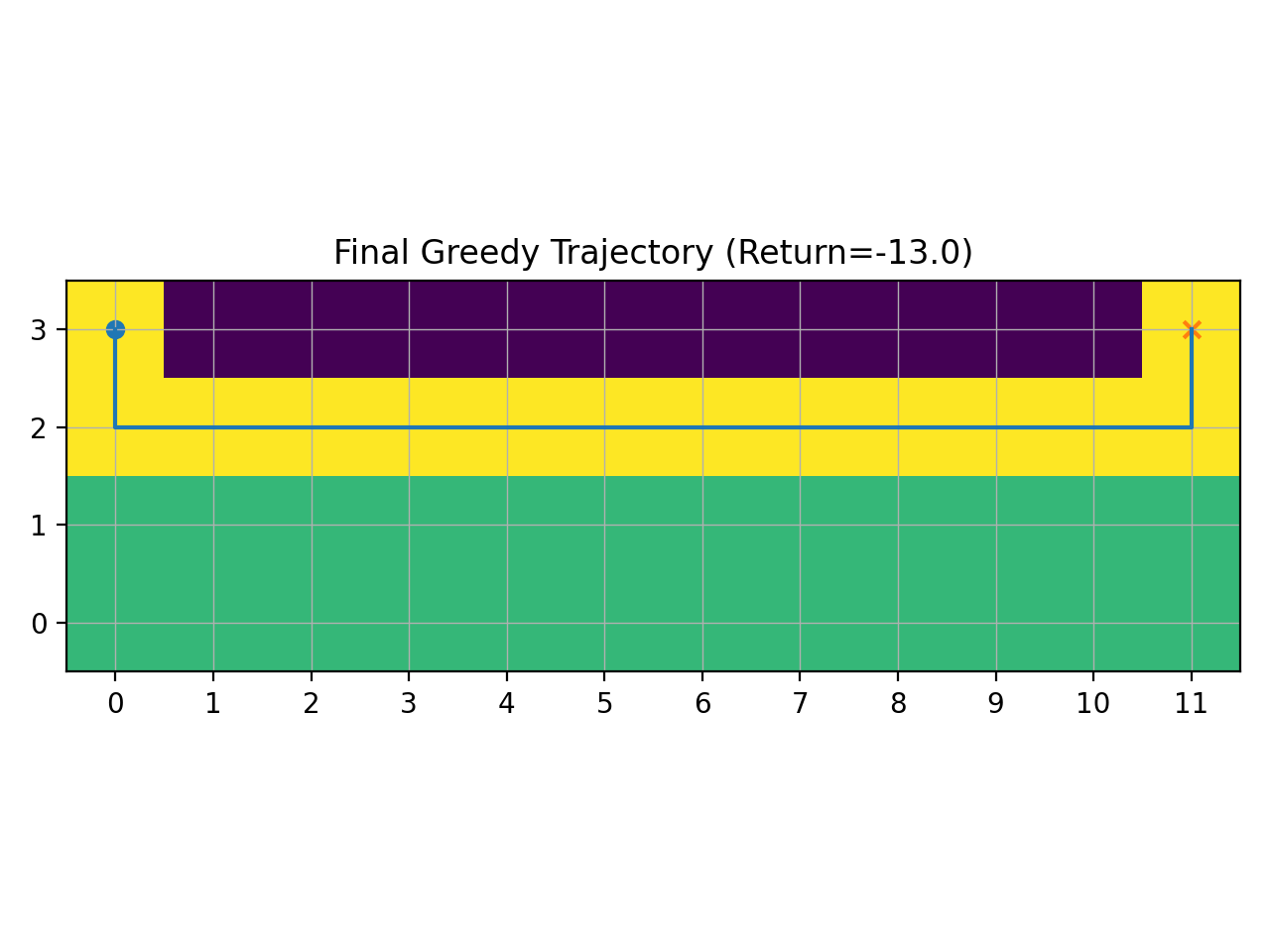
说明
探索率ε越大,智能体越常随机试探,前期更容易跳出坏策略,但回报曲线上升更慢且波动大;ε过小则更快收敛,却可能过早陷入次优路径。采用随训练递减的ε,可在早期充分探索、后期稳定利用,从而得到更短更安全的路径与更高回报。

