为什么需要线段树
问题背景:在数组上频繁的做区间操作
常见数据结构对比:
建树
结点 u 将其左儿子 2*u 和右儿子 2*u+1 组成的区间进行管理。 n 个节点一般需要 4*n 的空间来进行存储。
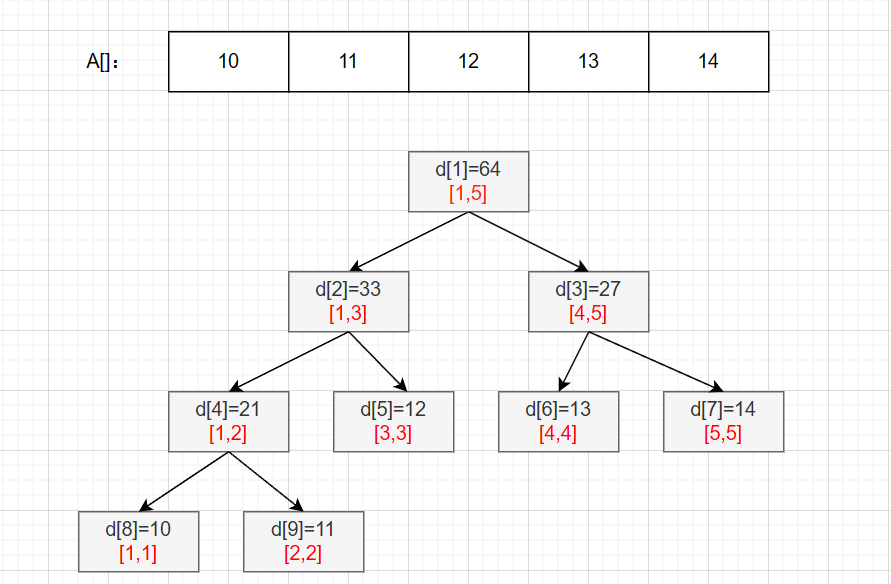
自底向上,把小区间信息合并成大区间的信息。
void build(int u, int l, int r, const vector<ll> &a)
{
if (l == r)
{
tree_sum[u] = a[l];
return;
}
else
{
int mid = (l + r) >> 1;
build(u << 1, l, mid, a);
build(u << 1 | 1, mid + 1, r, a);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
}
}区间查询
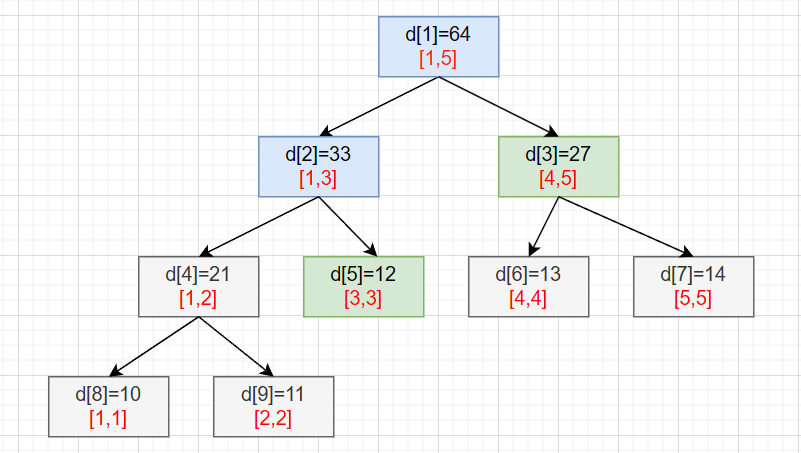
把查询区间拆成若干个完全覆盖的子区间,累加答案。
如上图所示:
要查询区间 [3,5] 时,遇到右子树 [4,5] 该区间完全包含直接返回该子树的和;
左子树 [1,3] 没有完全包含,继续向下查找,遇到 [1,2] 完全不包含,返回;
遇到 [3,3] 完全包含,返回该子树的值。
这样就在 logn 的时间内完成了对区间的查询。
ll range_query(int u, int l, int r, int L, int R)
{
if (R < l || L > r)
{ // Not included at all
return 0;
}
if (L <= l && r <= R)
{ // Completely included
return tree_sum[u];
}
push_down(u, l, r);
int mid = (l + r) >> 1;
ll res = 0;
if (L <= mid)
res += range_query(u << 1, l, mid, L, R);
if (R > mid)
res += range_query(u << 1 | 1, mid + 1, r, L, R);
return res;
}区间修改
懒标记(Lazy)
把修改“先记在结点上”,暂时不往下传,等之后真正需要访问子结点时再推下去。
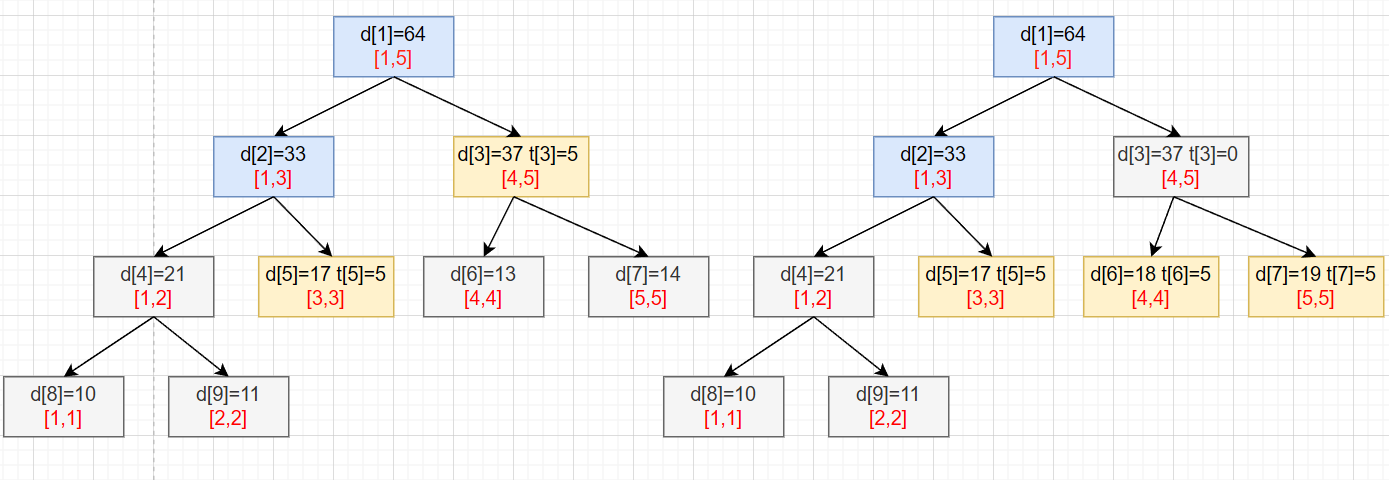
我们假设要对区间 [3,5] 进行区间加 5:
我们递归到完全覆盖的区间是,对结点打上标记,并对该结点值进行操作,操作的值就是其儿子们的贡献 ;
当区间递归到 [4,5] 时, t[3]=5、d[3]=27+5*2=37
当区间递归到 [3,3] 时, t[5]=5、d[5]=12+5=17
打上的标记是为了下一次查询到该节点时,知道此节点有标记,需要向下传递 pushdown 操作,从而在取消当前节点的懒标记,将标记下传。
如右图,查询区间 [3,5] 时,在遇到区间 [4,5] 时,会将懒标记下传,从而不影响下次的操作。
void apply_add(int u, int l, int r, ll val)
{
tree_sum[u] += val * (r - l + 1);
if (l != r)
{
lazy_add[u] += val;
}
}
// pushdown the lazy tag
void push_down(int u, int l, int r)
{
if (lazy_add[u] != 0)
{
int mid = (l + r) >> 1;
ll tag = lazy_add[u];
apply_add(u << 1, l, mid, tag);
apply_add(u << 1 | 1, mid + 1, r, tag);
lazy_add[u] = 0;
}
}
// add value to the interval
void range_add(int u, int l, int r, int L, int R, ll val)
{
if (R < l || r < L)
{
return;
}
if (L <= l && r <= R)
{
apply_add(u, l, r, val);
return;
}
push_down(u, l, r);
int mid = (l + r) >> 1;
if (L <= mid)
range_add(u << 1, l, mid, L, R, val);
if (R > mid)
range_add(u << 1 | 1, mid + 1, r, L, R, val);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
}例题
区间修改+单点修改+区间取模+区间查询
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int INF = 1e9;
struct SegmentTree
{
int n;
vector<ll> tree_sum;
vector<ll> tree_max;
vector<ll> lazy_add;
SegmentTree(int n = 0)
{
init(n);
}
void init(int n_)
{
n = n_;
tree_sum.assign(4 * n, 0);
tree_max.assign(4 * n, 0);
lazy_add.assign(4 * n, 0);
}
// build Tree
void build(int u, int l, int r, const vector<ll> &a)
{
if (l == r)
{
tree_sum[u] = a[l];
tree_max[u] = a[l];
return;
}
else
{
int mid = (l + r) >> 1;
build(u << 1, l, mid, a);
build(u << 1 | 1, mid + 1, r, a);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
tree_max[u] = max(tree_max[u << 1], tree_max[u << 1 | 1]);
}
}
// apply the interval increment to the current node;
void apply_add(int u, int l, int r, ll val)
{
tree_sum[u] += val * (r - l + 1);
tree_max[u] += val;
if (l != r)
{
lazy_add[u] += val;
}
}
// pushdown the lazy tag
void push_down(int u, int l, int r)
{
if (lazy_add[u] != 0)
{
int mid = (l + r) >> 1;
ll tag = lazy_add[u];
apply_add(u << 1, l, mid, tag);
apply_add(u << 1 | 1, mid + 1, r, tag);
lazy_add[u] = 0;
}
}
// add value to the interval
void range_add(int u, int l, int r, int L, int R, ll val)
{
if (R < l || r < L)
{
return;
}
if (L <= l && r <= R)
{
apply_add(u, l, r, val);
return;
}
push_down(u, l, r);
int mid = (l + r) >> 1;
if (L <= mid)
range_add(u << 1, l, mid, L, R, val);
if (R > mid)
range_add(u << 1 | 1, mid + 1, r, L, R, val);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
tree_max[u] = max(tree_max[u << 1], tree_max[u << 1 | 1]);
}
// mod value to the interval
void range_mod(int u, int l, int r, int L, int R, ll mod)
{
if (R < l || r < L)
{
return;
}
if (tree_max[u] < mod)
{
return;
}
if (l == r)
{
tree_sum[u] %= mod;
tree_max[u] = tree_sum[u];
lazy_add[u] = 0;
return;
}
push_down(u, l, r);
int mid = (l + r) >> 1;
if (L <= mid)
range_mod(u << 1, l, mid, L, R, mod);
if (R > mid)
range_mod(u << 1 | 1, mid + 1, r, L, R, mod);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
tree_max[u] = max(tree_max[u << 1], tree_max[u << 1 | 1]);
}
// update by a single value
void update_singleValue(int u, int l, int r, int pos, ll val)
{
if (l == r)
{
tree_sum[u] = val;
tree_max[u] = val;
lazy_add[u] = 0;
return;
}
push_down(u, l, r);
int mid = (l + r) >> 1;
if (pos <= mid)
update_singleValue(u << 1, l, mid, pos, val);
else
update_singleValue(u << 1 | 1, mid + 1, r, pos, val);
tree_sum[u] = tree_sum[u << 1] + tree_sum[u << 1 | 1];
tree_max[u] = max(tree_max[u << 1], tree_max[u << 1 | 1]);
}
// query by the interval of [L,R]
ll range_query(int u, int l, int r, int L, int R)
{
if (R < l || L > r)
{ // Not included at all
return 0;
}
if (L <= l && r <= R)
{ // Completely included
return tree_sum[u];
}
push_down(u, l, r);
int mid = (l + r) >> 1;
ll res = 0;
if (L <= mid)
res += range_query(u << 1, l, mid, L, R);
if (R > mid)
res += range_query(u << 1 | 1, mid + 1, r, L, R);
return res;
}
};
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
SegmentTree st(n);
st.build(1, 1, n, a);
while (m--)
{
int op;
int l, r;
cin >> op;
if (op == 0)
{
ll k;
cin >> l >> r >> k;
st.range_add(1, 1, n, l, r, k);
}
else if (op == 1)
{
cin >> l >> r;
cout << st.range_query(1, 1, n, l, r) << endl;
}
else if (op == 2)
{
int pos;
ll x;
cin >> pos >> x;
st.update_singleValue(1, 1, n, pos, x);
}
else if (op == 3)
{
ll x;
cin >> l >> r >> x;
st.range_mod(1, 1, n, l, r, x);
}
}
return 0;
}
