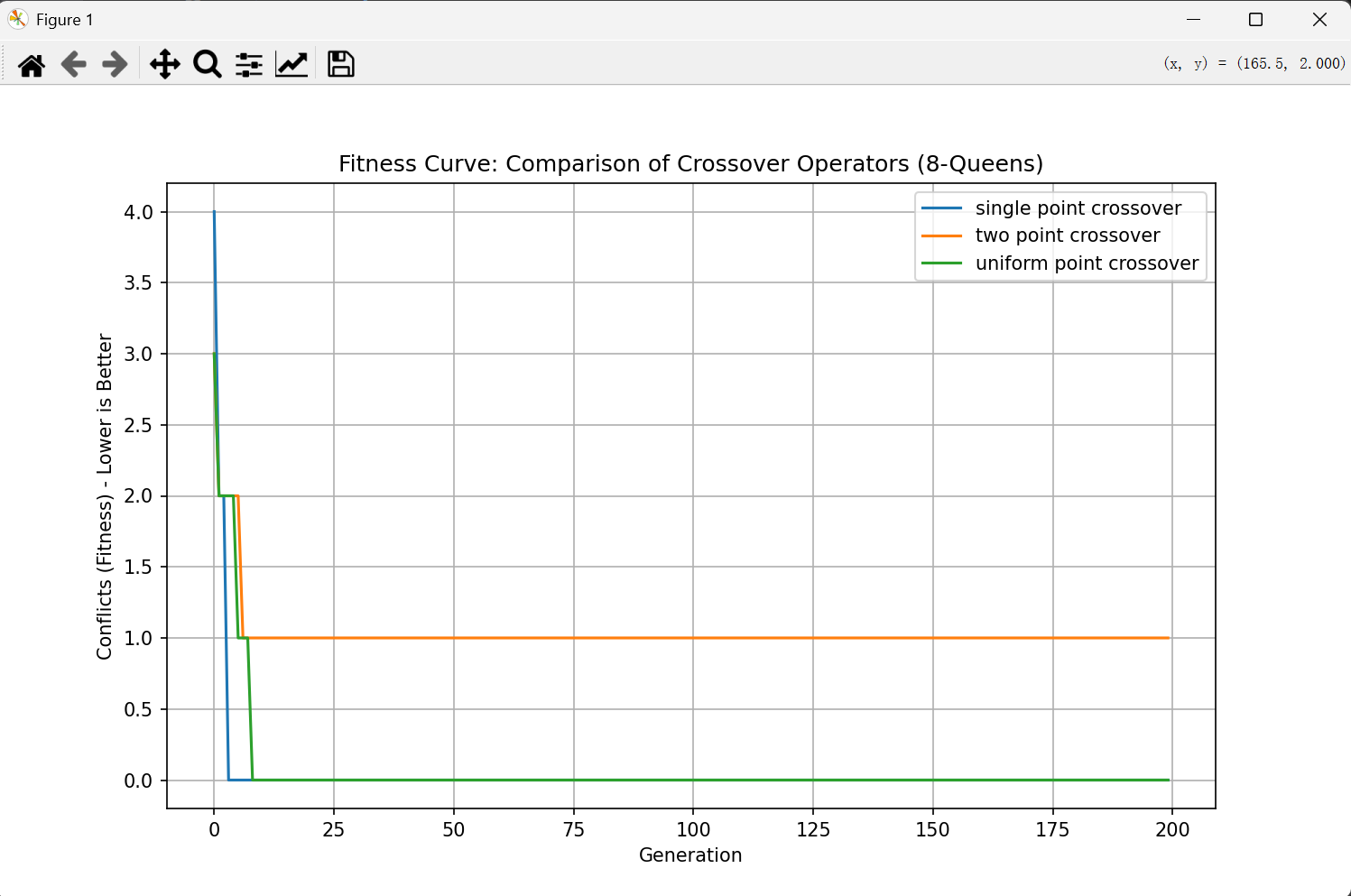
实现 GA 求解 8 皇后问题,观察代数变化曲线。
输出:应度曲线、最优路径或棋盘状态。
对比不同交叉算子(单点、双点、均匀)。
-
编码方式:采用整数编码(数组索引代表行,数值代表列)。
-
适应度函数:计算冲突数(列冲突 + 对角线冲突),目标是最小化冲突(最优为 0)。
-
三种交叉算子:单点 (Single-point)、双点 (Two-point)、均匀 (Uniform)。
-
可视化:使用
matplotlib绘制三者的适应度下降曲线,并输出最终的棋盘形态。
Code
import random
import numpy as np
import matplotlib.pyplot as plt
import copy
# --- 配置参数 ---
N_QUEENS = 8 # 8皇后
POP_SIZE = 100 # 种群大小
MAX_GEN = 200 # 最大迭代次数
MUTATION_RATE = 0.05 # 变异率
CROSSOVER_RATE = 0.8 # 交叉率
class GeneticNQueens:
def __init__(self, crossover_type='single'):
self.crossover_type = crossover_type
# 初始化种群:每个个体是一个长度为8的数组,值域0-7
self.population = [np.random.randint(0, N_QUEENS, N_QUEENS) for _ in range(POP_SIZE)]
self.history = [] # 记录每代的最佳适应度
def get_fitness(self, individual):
"""
计算适应度(冲突数)。越低越好,0表示无冲突。
"""
conflicts = 0
n = len(individual)
# 检查列冲突和对角线冲突
# 注意:行冲突由编码方式避免了(索引即行号)
for i in range(n):
for j in range(i + 1, n):
# 列冲突
if individual[i] == individual[j]:
conflicts += 1
# 对角线冲突 (行差 == 列差)
elif abs(i - j) == abs(individual[i] - individual[j]):
conflicts += 1
return conflicts
def selection(self):
"""锦标赛选择"""
tournament_size = 5
candidates = random.sample(self.population, tournament_size)
candidates.sort(key=lambda x: self.get_fitness(x))
return copy.deepcopy(candidates[0])
def crossover(self, p1, p2):
"""
根据指定的类型执行交叉
"""
if random.random() > CROSSOVER_RATE:
return p1, p2
c1, c2 = copy.deepcopy(p1), copy.deepcopy(p2)
size = len(p1)
if self.crossover_type == 'single':
# 单点交叉
point = random.randint(1, size - 1)
c1 = np.concatenate((p1[:point], p2[point:]))
c2 = np.concatenate((p2[:point], p1[point:]))
elif self.crossover_type == 'two':
# 双点交叉
point1 = random.randint(1, size - 2)
point2 = random.randint(point1 + 1, size - 1)
c1 = np.concatenate((p1[:point1], p2[point1:point2], p1[point2:]))
c2 = np.concatenate((p2[:point1], p1[point1:point2], p2[point2:]))
elif self.crossover_type == 'uniform':
# 均匀交叉
for i in range(size):
if random.random() > 0.5:
c1[i], c2[i] = p2[i], p1[i]
return c1, c2
def mutate(self, individual):
"""单点变异:随机改变某一行的皇后位置"""
if random.random() < MUTATION_RATE:
idx = random.randint(0, N_QUEENS - 1)
individual[idx] = random.randint(0, N_QUEENS - 1)
return individual
def run(self):
best_solution = None
min_conflicts = float('inf')
for gen in range(MAX_GEN):
# 1. 计算种群所有个体的适应度
scores = [self.get_fitness(ind) for ind in self.population]
# 记录当前最佳
current_best_score = min(scores)
self.history.append(current_best_score)
if current_best_score < min_conflicts:
min_conflicts = current_best_score
best_solution = self.population[scores.index(current_best_score)]
# 如果找到解(冲突为0),可以提前停止,但在对比实验中通常跑满代数
if min_conflicts == 0:
# 为了曲线长度一致,填充剩余代数
self.history.extend([0] * (MAX_GEN - gen - 1))
break
# 2. 生成新一代
new_population = []
while len(new_population) < POP_SIZE:
p1 = self.selection()
p2 = self.selection()
c1, c2 = self.crossover(p1, p2)
c1 = self.mutate(c1)
c2 = self.mutate(c2)
new_population.append(c1)
new_population.append(c2)
self.population = new_population[:POP_SIZE]
return best_solution, min_conflicts, self.history
# --- 主程序:运行并对比三种算子 ---
operators = ['single', 'two', 'uniform']
results = {}
print(f"{'算子类型':<10} | {'最终冲突数':<10} | {'最优解 (行0-7的列号)'}")
print("-" * 50)
for op in operators:
ga = GeneticNQueens(crossover_type=op)
best_sol, score, history = ga.run()
results[op] = {'history': history, 'solution': best_sol, 'score': score}
print(f"{op:<10} | {score:<10} | {best_sol}")
# --- 绘图 ---
plt.figure(figsize=(10, 6))
for op in operators:
plt.plot(results[op]['history'], label=f'{op} point crossover')
plt.title('Fitness Curve: Comparison of Crossover Operators (8-Queens)')
plt.xlabel('Generation')
plt.ylabel('Conflicts (Fitness) - Lower is Better')
plt.legend()
plt.grid(True)
plt.show()
# --- 打印最优棋盘 (以单点交叉的结果为例) ---
def print_board(solution):
print("\n=== 最优棋盘可视化 (示例) ===")
n = len(solution)
for row in range(n):
line = ""
for col in range(n):
if solution[row] == col:
line += " Q "
else:
line += " . "
print(line)
print("Coordinates:", list(enumerate(solution)))
# 如果找到了完美解,打印它
if results['uniform']['score'] == 0:
print_board(results['uniform']['solution'])
elif results['two']['score'] == 0:
print_board(results['two']['solution'])
else:
print_board(results['single']['solution'])
运行结果
算子类型 | 最终冲突数 | 最优解 (行0-7的列号)
--------------------------------------------------
single | 0 | [3 5 7 2 0 6 4 1]
two | 1 | [4 7 0 3 5 2 1 6]
uniform | 0 | [4 1 7 0 3 6 2 5]可视化